
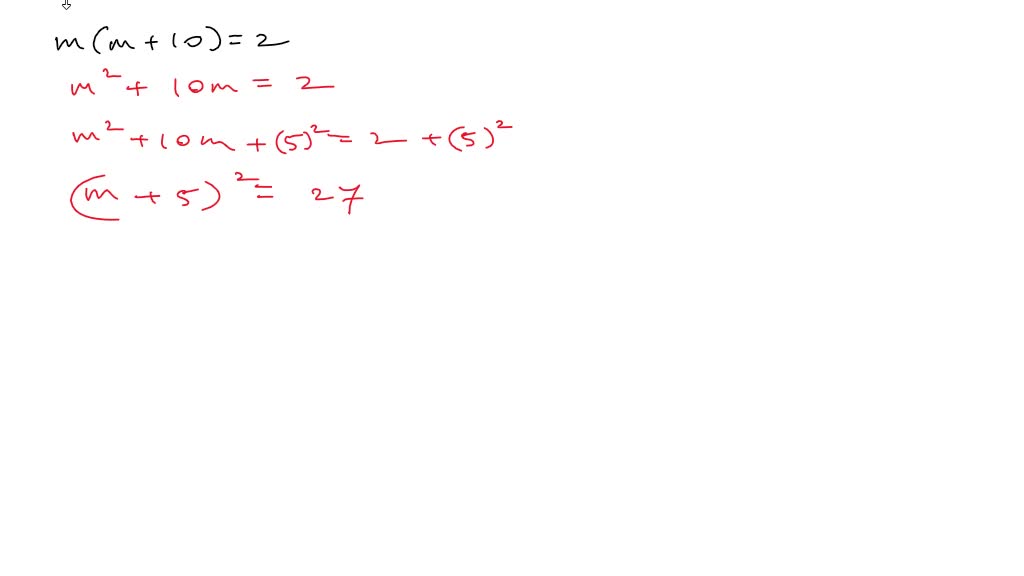
The solution set for two equations in three variables is, in general, a line. The solution set is the intersection of these hyperplanes, and is a flat, which may have any dimension lower than n.


įor n variables, each linear equation determines a hyperplane in n-dimensional space. For example, as three parallel planes do not have a common point, the solution set of their equations is empty the solution set of the equations of three planes intersecting at a point is single point if three planes pass through two points, their equations have at least two common solutions in fact the solution set is infinite and consists in all the line passing through these points. Thus the solution set may be a plane, a line, a single point, or the empty set. Because a solution to a linear system must satisfy all of the equations, the solution set is the intersection of these lines, and is hence either a line, a single point, or the empty set.įor three variables, each linear equation determines a plane in three-dimensional space, and the solution set is the intersection of these planes. The system has a single unique solution.įor a system involving two variables ( x and y), each linear equation determines a line on the xy- plane.The system has infinitely many solutions.The set of all possible solutions is called the solution set.Ī linear system may behave in any one of three possible ways: , x n such that each of the equations is satisfied. The solution set for the equations x − y = −1 and 3 x + y = 9 is the single point (2, 3).Ī solution of a linear system is an assignment of values to the variables x 1, x 2. The number of vectors in a basis for the span is now expressed as the rank of the matrix. To see examples on how to solve a system of linear equations by graphing as well as examples of “no solution” and “infinitely many solutions” check out my video tutorial below.A linear system in three variables determines a collection of planes The intersection point is the solution. The easiest and most visual way to find the intersection of a system is by graphing the equations on the same coordinate plane.
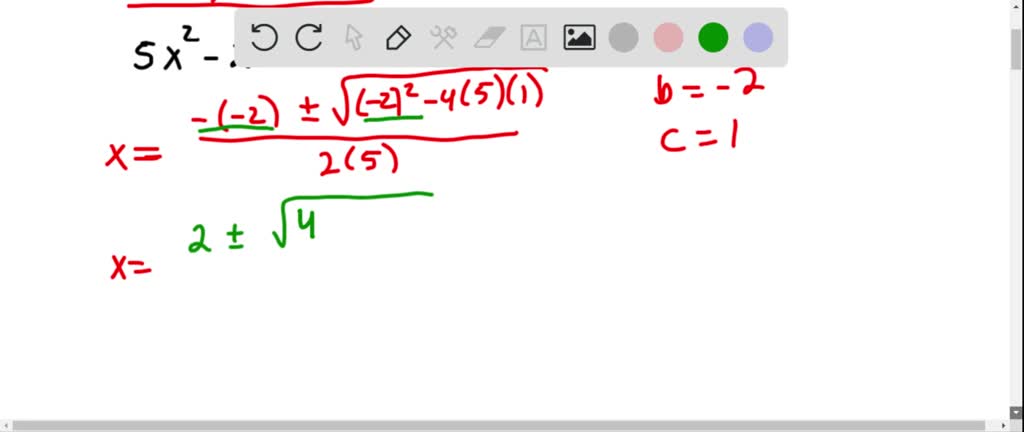
In this case, you’ll have infinitely many solutions. You also may encounter equations that look different, but when reduced end up being the same equation. Parallel lines by definition will never intersect, therefore they have no solution. Potential SolutionsĪs you may already realize, not all lines will intersect in exactly one point. For example, the solution to a system of two linear equations, the most common type of system, is the intersection point between the two lines. These may involve higher-order functions like quadratics, more than two equations in the system, or equations involving x, y, and z variables (these equations represent planes in 3D space).īut no matter how complicated your system gets, your solution always represents the same concept: intersection. That means your equations will involve at most an x-variable, y-variable, and constant value.Įventually (perhaps in algebra 2, precalculus, or linear algebra) you’ll encounter more complicated systems. When you first encounter system of equations problems you’ll be solving problems involving 2 linear equations. It’s a system, meaning 2 or more, equations. What is a System of Equations?Ī System of Equations is exactly what it says it is. Before you jump into learning how to solve for those unknowns, it’s important to know exactly what these solutions mean.


 0 kommentar(er)
0 kommentar(er)
